[머신러닝] [Python] Logistic Regression (로지스틱 회귀)
업데이트:
이번 포스팅에서는 Categorical 변수를 예측하는 모델인 Logistic Regression ( 로지스틱 회귀)에 대해 살펴보겠습니다. 포스팅에서 사용된 자료에 대해서는 가천대학교 소프트웨어학과 김원 교수님의 강의를 기반으로 작성되었음을 밝힙니다.
✅ Linear Regression ( 선형 회귀 )
Logistic Regression에 대한 설명에 앞서 기본적인 이해를 위해 선형 회귀에 대해서 간단하게 알아보겠습니다.
시험 공부하는 시간을 늘리면 늘릴 수록 성적이 잘 나옵니다. 하루에 걷는 횟수를 늘릴 수록, 몸무게는 줄어듭니다. 집의 평수가 클수록, 집의 매매 가격은 비싼 경향이 있습니다. 이는 수학적으로 생각해보면 어떤 요인의 수치에 따라서 특정 요인의 수치가 영향을 받고있다고 말할 수 있습니다. 조금 더 수학적인 표현을 써보면 어떤 변수의 값에 따라서 특정 변수의 값이 영향을 받고 있다고 볼 수 있습니다. 다른 변수의 값을 변하게 하는 변수를 x, 변수 x에 의해서 값이 종속적으로 변하는 변수 y라고 해봅시다.
이때 변수 x의 값은 독립적으로 변할 수 있는 것에 반해, y값은 계속해서 x의 값에 의해서, 종속적으로 결정되므로 x를 독립 변수, y를 종속 변수라고도 합니다. 선형 회귀는 한 개 이상의 독립 변수 x와 y의 선형 관계를 모델링합니다. 만약, 독립 변수 x가 1개라면 단순 선형 회귀라고 합니다.
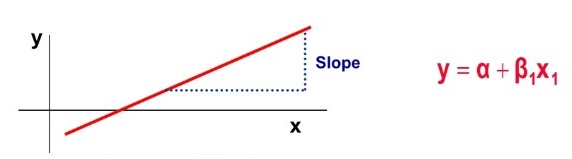
생각해보니 집의 매매가격은 단순히 집의 평수가 크다고 결정되는 것이 아니라, 집의 층수, 방의 개수, 역세권인지 아닌지 등 여러가지 요소에 영향을 많이 받는것 같습니다. 이제 이러한 다수의 요소를 가지고 집의 매매 가격을 예측해 보고 싶습니다. y(집의 매매가격)는 여전히 1개이지만 x(층수, 방개수, 역세권 등)는 여러개가 되었습니다. 이를 Multiple Linear Regression (다중 선형 회귀)라고 부릅니다.
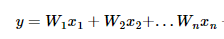
✅ Logistic Regression ( 로지스틱 회귀)
Logistic Regression은 데이터가 어떤 범주에 속할 확률을 0에서 1사이의 값으로 예측하고 그 확률에 따라 가능성이 더 높은 범주에 속하는 것으로 분류해주는 지도 학습 알고리즘이다.
스펨 메일 분류기 같은 예시를 생각하면 쉬운데, 어떤 메일을 받았을 때 그 메일이 스팸일 확률이 0.5이상이면 스팸으로 분류하고, 메일이 스팸일 확률이 0.5보다 낮으면 일반 메일로 분류하는 것이다. 이렇게 데이터가 2개의 범주 중 하나에 속하도록 결정하는 것을 Binary Classification (2진 분류)라고 한다.
로지스틱 회귀 역시 X와 Y의 관계식으로 설명 할 수 있는데, X는 Binary(양분된), Categorical(범주형), Continuous(연속형) 한 데이터 모두를 가질 수 있지만, Y는 Binary한 데이터만을 가질 수 있다.
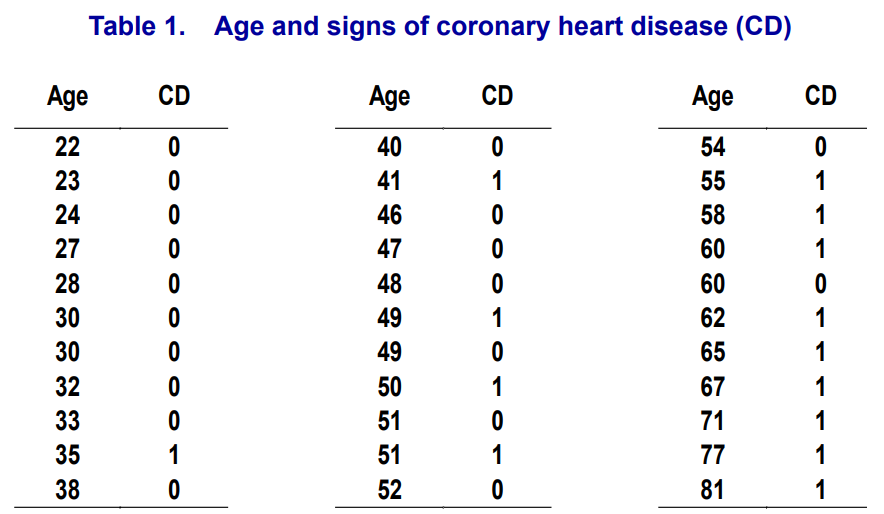
예시를 보며 자세히 살펴보자. X로 Age가 주어졌고 Y로는 심장병 유무가 주어진 데이터셋이다.
이를 Linear Regression으로 나타내면 아래 그림과 같다.
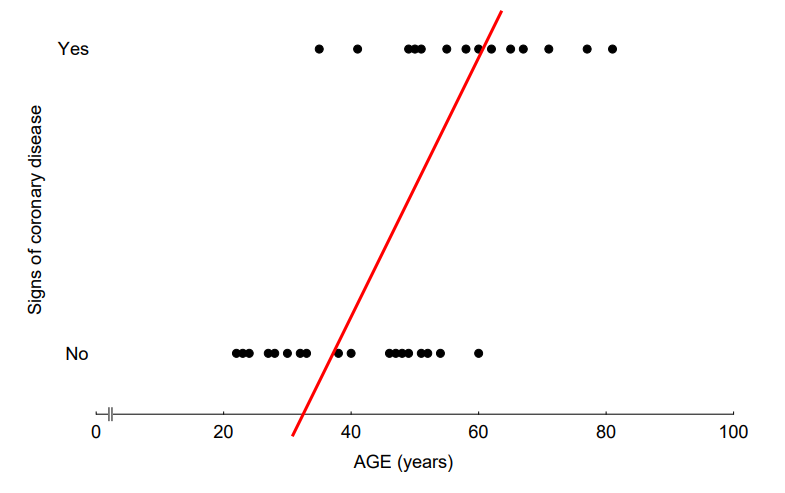
한눈에 보기에도 이상하다. Y가 Binary한 데이터로 주어졌기 때문에 Linear Regression으로 표현하면 정확도가 떨어지는 문제가 발생한다. 이를 해결하기 위해 데이터셋을 일부 수정한 뒤 Logistic Regression으로 나타내 보겠다.
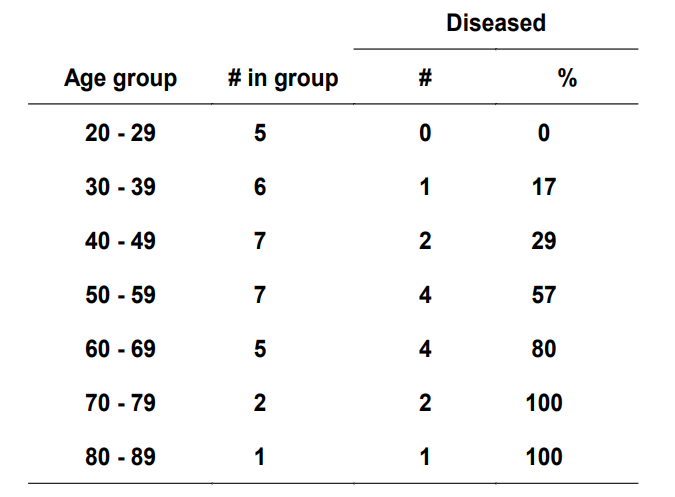
X로 주어진 Age를 나이대별로 묶은 뒤 심장병에 걸린 사람수를 나타낸 데이터셋이다. 이를 Logistic Regression으로 나타내면 아래 그림과 같다.
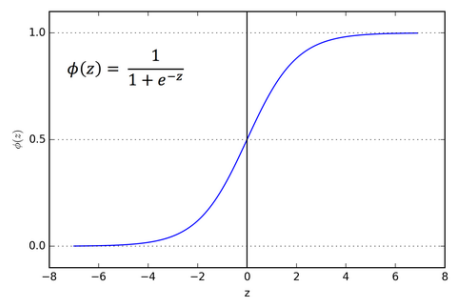
Y값은 0~1사이의 값으로 표현되며 y<0.5일때는 0으로 치환되고 y>=0.5일때는 1로 치환되는 결과를 보여준다. 위의 그래프처럼 나타내는 것을 Sigmoid Function (시그모이드 함수) 이라고 부른다.
이처럼 Y가 Binary한 데이터로 주어질때는 Linear Regression을 사용하는 것 보다는 Logistic Regression을 사용하는 것이 훨씬 정확도가 높다.
✅ Logit(로짓) - log + odds
Logistic Regression을 구현하는 것은 어렵지 않다. 파이썬에 있는 scikit-learn 라이브러리를 사용하면 코드 몇줄로 바로 구현할 수 있다. 그러나 그 작동 원리를 알고 구현하는 것과 모른채 blackbox식으로 구현하는 것은 엄연히 다르다. Logistic Regression의 작동 원리를 공부하기 위해 선행되어 알아야만 하는 몇가지 Keyword를 소개하겠다.
📌 Odds
Odds는 어떤 사건이 발생할 확률을 발생하지 않을 확률로 나눈 값을 의미한다. 어떤 사건이 일어날 확률을 p라고 했을때 Odds값은 p / (1-p) 이다.
예를 들어 p가 0.2라면 Odds = 0.2 / (1 - 0.8) = 0.25 이다.
📌 Odds Ratio
Odds Ratio는 두개의 Odds의 비율을 나타내는 값이다. 예를들어 Odds1 = 0.25 이고 Odds2 = 0.30이면 Odds Ratio = 0.25 / 0.30 = 0.833이다.
📌 Logit
사실상 Logit을 설명하기 위해 앞서 Odds와 Odds Ratio를 소개했다고 봐도 무방하다. 확률 p의 Logit은 다음과 같이 정의된다.

즉, Odds에 자연로그를 씌운 형태로 Logit이라는 말이 Log + Odds에서 나온말이다. 예를들어, p=0.5라고 하면 Odds = 0.5 / 0.5 = 1, Logit = ln(1) = 0 이된다.
✅ Solver Algorithms for Logistic Regression
파이썬의 Scikit-Learn에서는 다섯개의 알고리즘으로 Logic Regression을 해결한다. 각각의 알고리즘이 어떤식으로 동작하는지는 내용이 너무 방대하므로 설명하지 않겠고 그냥 이런게 있구나 하고 넘어가면 좋을 것 같다.
- newton-cg
- lbfgs
- liblinear
- sag
- saga
✅ Logistic Regression Python Code
이제 로지스틱 회귀를 파이썬으로 직접 구현하는 연습을 해보자.
📌 1. 데이터 불러오기
먼저 seaborn에 내재된 타이타닉 데이터셋을 불러오도록 하자.
import seaborn as sns
passengers = sns.load_dataset('titanic')
print(passengers.shape)
print(passengers.head())
총 891명의 데이터가 있고 총 15개의 컬럼이 있는걸 확인했다.

우리의 Target 데이터는 survived 이다. 살았는지 죽었는지 확인하는 컬럼이고 1은 생존, 0는 사망을 의미한다.
📌 2. 데이터 전처리
분석에 사용할 Feature 선택
먼저 생존여부에 큰 영향을 미쳤을 것으로 예상되는 컬럼을 sex, age, pclass로 지정했다. 여성, 어린이, 1/2/3등석 순으로 살아남을 확률이 높다고 가정해본 것이다.
문자열을 숫자로 변환
sex는 male과 female로 설정되있으므로 이를 숫자 데이터 1과 0으로 바꿔주자. 여성이 살아남을 확률이 높을것으로 예상하므로 남성을 0, 여성을 1이라고 바꿔주자.
passengers['sex'] = passengers['sex'].map({'female':1,'male':0})
결측치 채워주기
데이터를 살펴보면 age가 비어있는 경우가 있다. 이는 age의 평균치로 대체하겠다.
passengers['age'].fillna(value=passengers['age'].mean(), inplace=True)
Feature 분리하기
pclass의 경우 1등석에 탔는지, 2등석에 탔는지 각각의 feature로 만들어주기 위해 컬럼을 새로 생성해 분류하겠다.
passengers['FirstClass'] = passengers['pclass'].apply(lambda x: 1 if x == 1 else 0)
passengers['SecondClass'] = passengers['pclass'].apply(lambda x: 1 if x == 2 else 0)
features = passengers[['sex', 'age', 'FirstClass', 'SecondClass']]
survival = passengers['survived']
📌 3. Train/Test set 분리하기
from sklearn.model_selection import train_test_split
train_features, test_features, train_labels, test_labels = train_test_split(features, survival)
📌 4. 데이터 정규화(Scaling) 하기
StandardScaler를 사용해 데이터를 정규화 하였다.
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
train_features = scaler.fit_transform(train_features)
test_features = scaler.transform(test_features)
📌 5. 모델 생성 및 평가하기
from sklearn.linear_model import LogisticRegression
model = LogisticRegression()
model.fit(train_features, train_labels)
model을 생성해 LogisticRegression 함수를 넣어주면 끝이다.
이제 학습세트로 정확도를 바로 알아보자.
print(model.score(train_features, train_labels))
결과 :
0.7919161676646707
79%의 정확도를 가진다고 나온다.
Test Set에서도 정확도를 확인해보자.
print(model.score(test_features, test_labels))
결과 :
0.766816143498
76%의 정확도를 가진다고 나온다.
이제 각 Feature들의 계수(Coefficients)를 확인해볼 차례이다. 어떤 Feature가 생존에 큰 영향을 주는지 확인해 볼 수 있다.
print(model.coef_)
결과 :
[[ 1.21512352 -0.34590989 0.99346516 0.49466482]]
sex, age, firstclass, secondclass 순으로 넣었으므로 그순서대로 확인해주면 된다. 성별은 1에 가까우므로 여자이고, 일등석 탑승 여부가 중요하다는 걸 알 수 있다. 반면에 나이는 음수가 나오는데 이는 나이가 많을수록 생존 확률이 낮아진다는 의미로 해석할 수 있다.
📌 6. 예측하기
이번에는 새로운 임의의 데이터를 넣어서 예측해보자.
Jack = np.array([0.0, 20.0, 0.0, 0.0])
Rose = np.array([1.0, 17.0, 1.0, 0.0])
ME = np.array([0.0, 32.0, 1.0, 0.0])
sample_passengers = np.array([Jack, Rose, ME])
이제 스케일링을 다시해주자.
sample_passengers = scaler.transform(sample_passengers)
마지막으로 예측을 해보자.
print(model.predict(sample_passengers))
print(model.predict_proba(sample_passengers))
[0 1 0]
[[0.88995985 0.11004015]
[0.05240318 0.94759682]
[0.51644668 0.48355332]]
Jack과 나는 죽고 Rose만 산다..

댓글남기기